Quantifiying Process Rates
Denudation
Denudation rates for a surface can be calculated if the nuclide system is in secular equilibrium such that inputs equal outputs. This can be done for individual landforms such as bedrock tors, surface sediments; however these point observations are unlikely to give an adequate representation of denudation across an entire landscape. Luckily, a natural amalgamator exists in most landscapes, the river.
Fluvial sediment is a collection of debris derived from all parts of a drainage basin. A number of studies (Brown et al., 1995, Birerman and Steig, 1996, and Granger et al., 1996) were able to show that the nuclide concentration in a sample of river sand is the flux-weighted average of the nuclide concentration rates from all points in the drainage basin. Because of this, river sand can be used to determine basin-averaged denudation rates.
We'll start the discussion of denudation rates with the simple erosion of bedrock. The surface nuclide concentration, N(t), of an eroding surface is proportional to the production rate, P(0), and the inverse of the erosion rate, ε:
where λ is the half-life, ρ is the density of the surface material, and Λ is the mean free path length. If nuclide production and surface denudation occur for a long enough period of time (e.g t >> ρ ε / Λ) then the surface nuclide concentration remains constant with time, and:
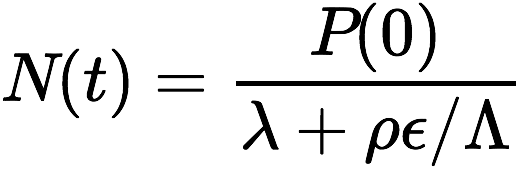
This is the basic steady-state equation governing cosmogenic nuclide derived denudation rates. These denudation rates are applicable over the averaging timescale, defined as the length of time required to remove one attenuation depth, where attenuation depth, z* (z* = ρ / Λ), is typically between 50 and 70 cm for common rock types. This averaging timescale is inversely proportional to the denudation rate (e.g. faster denudation rates mean that a parcel of rock will spend less time within the upper ~60 cm of rock, and vice versa).
 |  | |
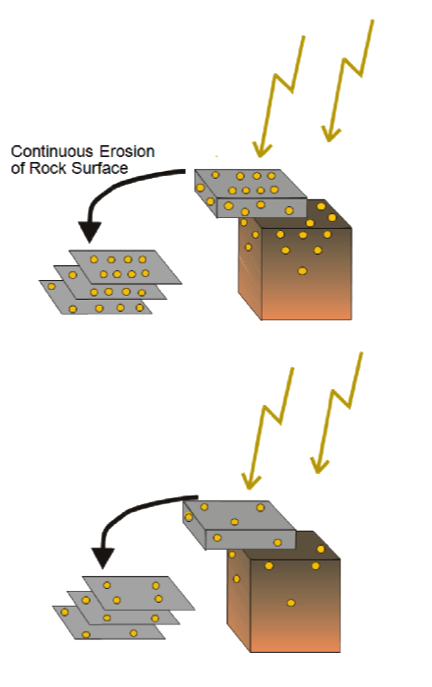| Steady state surface erosion. For slow surface denudation rates, eroded material contains high nuclides concentrations (top), for fast surface denudation rates, the eroded material contains low nuclide concentrations (bottom). | The averaging time scale of denudation rate measurements is inversely proportional to the denudation rate. From Dunai (2001) and based on von Blanckenburg (2005). |
We will take a brief pause to discuss the concept of a denudation rate. Cosmogenic nuclide derived rates are often erroneously termed erosion rates. An erosion rate is the rate at which material is physically removed from the surface (be it by soil creep, splash, landslide, or rock fall). In addition to erosion, material may be removed by chemical processes.
Weathering is the chemical disintegration (and potentially eventual removal) of material. These two processes added together make up the total surface denudation, D = E + W. If chemical weathering is absent, or inactive in near surface materials, then the denudation rate measured by cosmogenic nuclides is also an erosion rate. Otherwise it is more appropriate to use to term "denudation rate".
In the case of constant soil thickness, the denudation rate is equivalent to the soil production rate. An alternative method for calculating soil production rate is to determine the "denudation rate" at the base of the soil (see Heimsath et al., 1997; 2000).
This brings us naturally to a discussion of surface material density. As stated above, if the soil thickness remains constant over the cosmogenic averaging time, then the surface denudation rate is equal to the soil production rate. In this case, the rate of bedrock lowering drives the system. We therefore calculate denudation rates using the local bedrock. In some situations however, the use of bedrock density is an inappropriate.
The simplest example is for alluvial terraces. In this case, the terrace material is not genetically linked to the underlying bedrock, and terrace denudation rates should be calculated using the density of the terrace material. Likewise, for extremely thick soils, in which the entire accumulation of nuclides takes place within the soil column or when the soils are relict, the soil density should be used.
Basin-averaged denudation rates:
Knowing the denudation rates of individual landforms is a large step towards understanding the geomorphic evolution of a landscape. The time and money necessary to study an entire region however make this approach impractical for most researchers. As mentioned above, it is also possible to let nature do the averaging, and obtain an average denudation rate for entire river catchments from stream sediments.
The basic principles remain the same as for the case of a single eroding landform. The basin-averaged approach works even with spatially variable denudation rates so long as all portions of the catchment provide quartz in proportion to their denudation rate (e.g. areas, Ai, with slow denudation rates, Ei, deliver much less quartz with much higher nuclide concentrations, Ni, than quickly eroding surfaces);
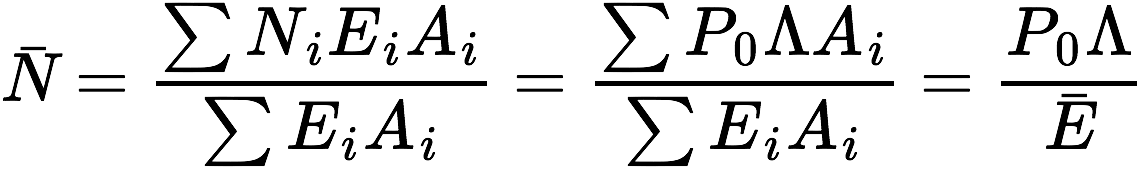(note that radioactive decay is left out for clarity)
There are, however, important caveats to the basin-averaging method (von Blanckenburg, 2005). These assumptions are:
(1) Erosion rate is constant through time such that cosmogenic steady state can be achieved.
(2) All subcatchments contribute sediment to the stream in proportion to their denudation rates.
(3) No grain size differences occur due to either bedrock distribution or preferential release by denudational processes.
(4) Quartz is not enriched in soils though time.
(5) Storage time, i.e. time spent on the hillslopes after initial erosion, is less than transport time.
(6) The erosional timescale (apparent age) is less than the decay timescale for the nuclide in question. This corresponds to ~0.5 mm ky-1 for 10Be, where λ ≈ 5 x 10-7 yr-1 and the absorption depth scale is 700 mm.
(7) Finally, as mentioned by Birerman and Steig (1996), quartz should be equally abundant in the contributing lithologies.
Many of these assumptions can be accounted for if enough information is available, i.e. correcting for quartz abundances (Birerman and Steig, 1996) or quartz enrichment (Riebe et al., 2001).